1.水晶振動子マイクロバランス法とは1
水晶の結晶から特定の角度で薄板状に切り出し、その水晶切片の両面に金属薄膜を取り付けて電極としたものに交流電場を印加すると、その水晶切片に固有の共鳴周波数(基本振動数)で振動する性質を示すことから、こうした素子は水晶振動子(水晶発振子)と呼ばれています。
この金属薄膜表面に微量物質が吸着するとその質量に応じて基本振動数が減少することが知られており、水晶振動子はナノ・グラム・オーダーの微量天秤として利用されています。このような利用法は水晶振動子マイクロバランス(Quartz-crystal Microbalance; QCM)法といわれています。
2.水晶板を振動させる2-4
水晶切片が振動するしくみは、水晶結晶が有する圧電効果(結晶の力学歪みとその表面電位発生に依存性があること)に基づいています。
ある特定の角度で切り出した水晶切片の両面に電極を取り付けて水晶に電圧をかけると、水晶内のカチオンとアニオンの相対的な位置が変化し同時に結晶のずりひずみ(水晶板表面に対して平行な方向)が起こります。一方、印加した電圧を戻せばひずみは解消され元に戻ります。これらの現象を利用して、電圧印加のON/OFFを繰り返すとずり運動を継続(ずり振動)させることができます(図1)。
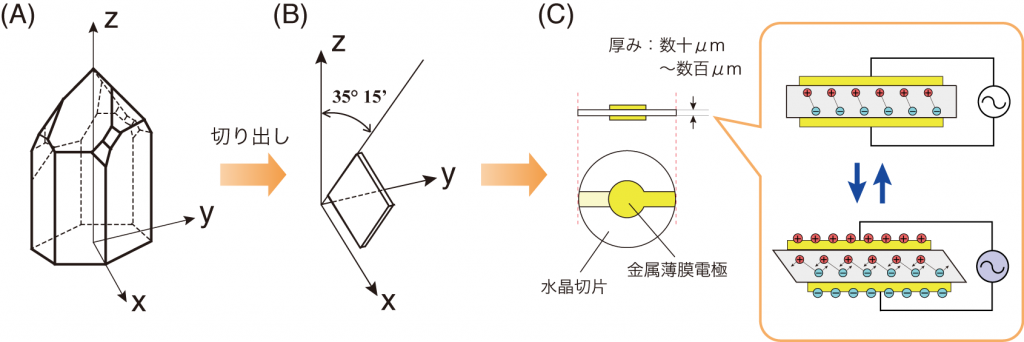
図1 (A) 水晶の結晶構造、(B)特定の角度による水晶切片の切り出し、および(C)水晶切片の両面に電極として金属薄膜をつけたものおよび振動電場を印加した時の水晶のずりひずみの概略図
電圧を印加してから結晶がずり歪みが完了するまでには、所定の時間を必要とする(主に水晶内の振動伝播速度と水晶板の厚みで決定され、厚みがあるほど時間がかかる)ので、水晶板のずり運動には厚みで決まる固有の周期を持つことになります。このとき印加する電圧の周期をずり運動の周期と同期させると、水晶板は振動子として一定の周期(振動数)で振動させつづけることができます。
この水晶板の振動現象は、重りのついたバネの振動、糸の先端に重りを付けた振り子の振動、ぴんと張った弦をはじいたときの振動などの力学的な振動現象と類似しており、印加電圧を水晶振動子と同期させる操作は、振り子の振動で最大振幅の位置でタイミング良く押し戻す操作を行っていることに相当します。実際、水晶振動子が常に振動するように帰還増幅型発振回路を用いてエネルギー供給すると、振動子は継続的に発振するようになります。
3.微量天秤としての水晶振動子3-7
一定の振動数で振動している水晶板の金属薄膜上に物質が吸着すると、その物質も水晶と共に振動することとなり実質的に水晶の運動エネルギーが転移することから、その吸着物質の質量に応じて系全体の振動数が減少します。
このときの振動数の変化が電極上に吸着した物質の質量に比例していることが1959年にSauerbreyによって報告されました。Sauerbreyは、振動数の変化ΔFと吸着物質の質量ΔMとの間に以下の関係式(Sauerbrey式)が成り立つことを報告しています8。
 (1)
(1)
ここで、ΔFは水晶振動子の振動数変化量(Hz)、F0は基本振動数(Hz)、Aは水晶板上の金属薄膜電極の面積、μq(=2.947×1011g cm-1s-2) は水晶の弾性率、ρq(=2.648 g cm-3) は水晶の密度、ΔMは電極に付着した物質の質量をそれぞれ表しています。
式(1)において(ΔM)/Aを単位面積あたりに付着した物質の質量Δmとして、残りの定数項をKとおくと式(2)のように簡単な比例式で表せます。
![]() (2)
(2)
すなわち、水晶振動子の振動数変化ΔF (Hz)をモニターすることでその電極上での物質の単位面積あたりの質量変化Δm (ng cm-2)を計測できることを示しています。
図2は基本的な水晶振動子およびその振動数変化を測定する装置の概略図です。水晶振動子を発振させるための帰還増幅型発振回路、発振している水晶振動子の振動数を計測する周波数カウンター、および周波数を記録するパソコンが主な構成要素です。
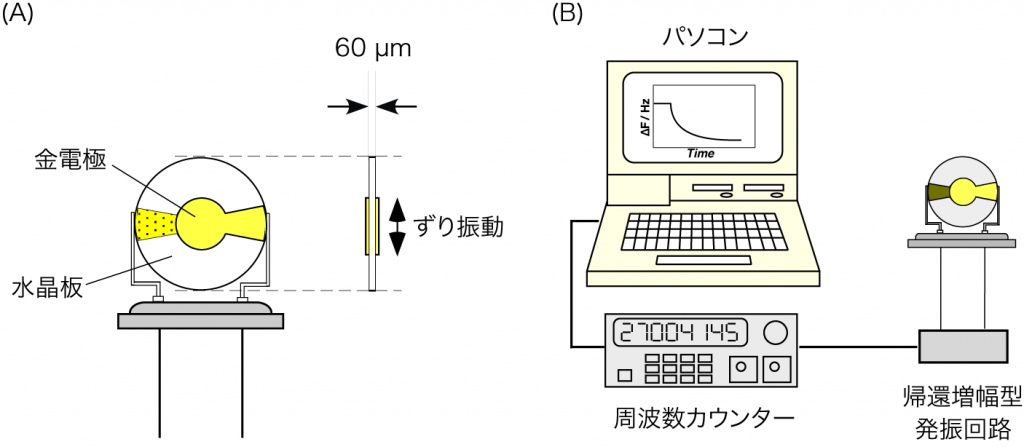
図 2 (A) 27 MHz水晶振動子の構造、(B)振動数変化測定装置の概略図
式(2)の係数Kは、水晶発振子の水晶の厚みに基づく基本振動数F0に依存する定数です。例えば、60μm厚の水晶板を用いた場合は、基本振動数はおよそ27 MHzとなり、係数Kを理論式より求めるとK= 1.65 Hz ng-1cm2となります。
実際に27 MHzの水晶発振子を用いてLB膜累積実験を行ったところ、求められた係数Kは、K= 1.62 Hz ng-1cm2となりました。これは、電極1 cm2あたりに約0.62 ngの物質が付着すると1 Hz振動数が減少することを示しています。
精度の高い周波数カウンターを使用すれば、周波数の検出は0.1〜0.01 Hz(サンプリング間隔0.1秒)の精度で測定することが可能なので、理論的な検出限界は1 ng cm-2以下ということになります。すなわち水晶振動子は、原子の単分子層吸着をも測定できるほど高感度であると言えます5。実際、水晶振動子は真空蒸着装置における蒸着膜の膜厚モニター用として実用化されています。
このような質量を計測することのできる水晶振動子は、通常の機械式天秤(balance)では不可能なナノグラム・オーダーの極微量の物質の質量を検出できる微量天秤(microbalance)ということから、QCM(Quartz-Crystal Microbalance:水晶振動子マイクロバランス)と呼ばれています。
4.バイオセンサーとしての利用
微量天秤として利用できることが明らかとなったQCMは、当初はガス分子を検出するガスセンサーなどQCMを気相中で使用することを前提として利用されてきました。一方、水中で使用するという試みはありましたが、水溶液のような粘性の高い物質と接するため振動が強く減衰されてしまい安定な発振が得られないこと、水晶振動子の構造自身が金属薄膜で絶縁体である水晶を挟んだ一種のコンデンサーであるため緩衝溶液中などでは両電極が短絡してしまうこと、などの構造的な問題がありそのままでの水中での利用は広がりませんでした。
1980年になって野村らは水中での金属イオンの検出にQCMを初めて使用し8、時を同じくしてKonashらはQCMを液体クロマトグラフィの検出器に初めて用いたことを報告しました9。発振回路の改良や、水晶振動子の片面(非検出面)を液に触れないように被覆するなどの改良があったことで水晶振動子の水相中での安定した発振が得られるようになったことが要因でした。こうして水相中でもQCMが機能することが示されたことから、QCMを水中でも使おうとする機運が出てきました。
バイオセンサーへの適用には定量的な点でまだ装置的な改良の必要性がありました。我々のグループでは1990年になって本格的にQCMのバイオセンサーへの応用を目指し、さまざまな生体分子間相互作用の検出にQCMの利用を検討し始めました10。
水晶板はハンドリングのしやすさと片側だけ液面と接するようにするために、片側のみシリコンカバーで被覆したセンサーチップを作製しました。装置としては生体分子を扱うことを考慮して温度管理や撹拌機能を持たせるために、ペルチェ素子上にアルミブロックを設置しその中にラウンド底のガラスセルをセットして、撹拌子により均一な系の中で測定ができる装置を自作しました(図3)。実際の測定では、水晶電極表面に受容体となる分子を固定しておき、マイクロピペットでサンプル分子をガラスセルに添加して、特定の分子が捕捉されたかどうかを基板上の質量増加としてモニターしてきました。質量変化として分子間相互作用を検出できることを原理として、さまざまな生体分子間相互作用の観察を行ってきました1。
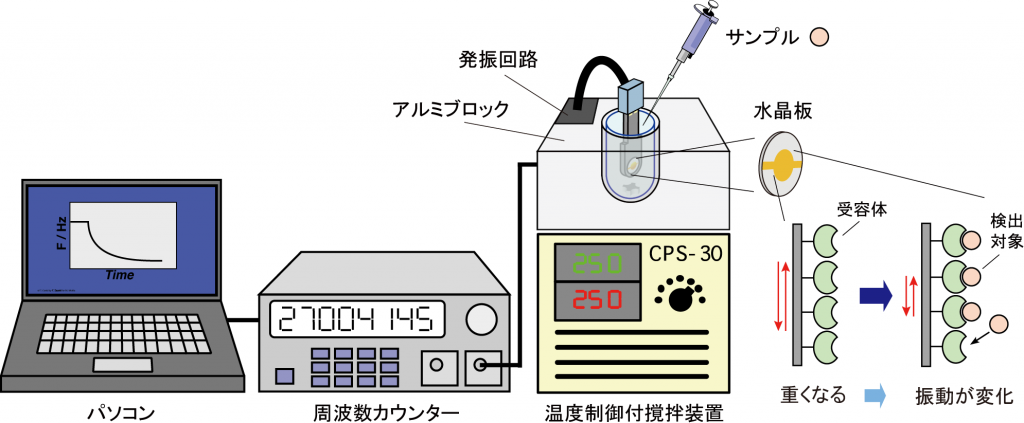
図3 バイオセンサー用に自作したQCM装置および基板上での分子間相互作用に基づく検出原理の概略図
5.QCM装置で測定できること
(1)生体分子間相互作用10-12
QCMの特徴は、基板上の質量変化(Δm)がわかることに加えて、1秒間隔でデータを取得できることです。基板上にゲスト分子を固定化しておき溶液側にホスト分子を添加すれば、ホスト-ゲストの分子間相互作用の経時的な様子が振動数(∆F)の減少として観察できます(図4)。
これまでにQCMを用いることで、ホストとして一本鎖DNAを固定したQCM基板上に相補的なDNA鎖をゲストとして添加しDNAの二重鎖形成過程を観察した例や、基板に固定した二本鎖DNA上への転写因子などの塩基配列特異的なタンパク質やペプチドの結合、膜タンパク質を固定した基板に膜タンパク質認識分子の結合など、さまざまな生体分子の相互作用が観察できることがわかりました。さらには結合速度定数konや解離速度定数koffを求める動力学解析ができることもわかりました。
基板上にどのようなホスト分子を固定するかでQCMの応用も広がります。抗体分子を固定して特定の分子を検出するバイオセンサーとしての利用や、特定の材料表面にタンパク質が吸着するかどうかを評価するといった評価装置としての利用法も考えられます。
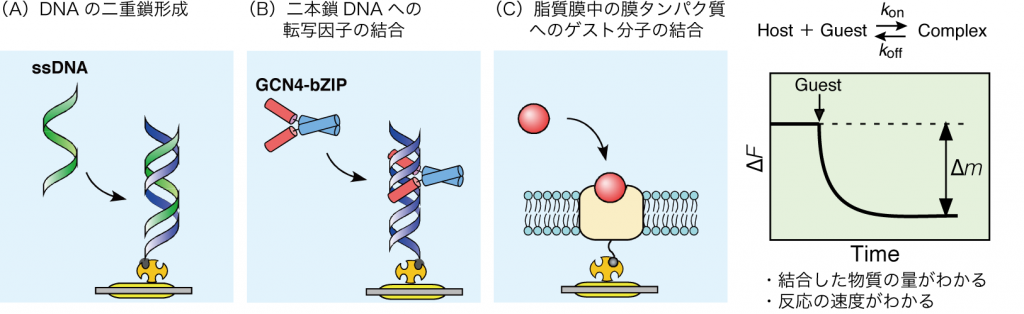
図4 生体分子間相互作用の測定例
(2)酵素反応解析13-16
QCM法は、基板上の質量が変化すればその様子を経時観察できるので、プロテアーゼなどの加水分解酵素やDNAポリメラーゼのような重合反応酵素などの反応追跡も可能になります。例えば、基板上に基質タンパク質を固定しておき、そこへプロテアーゼ(タンパク質加水分解酵素)を添加すると、酵素の基質への結合に伴う振動数(ΔF)の減少(質量の増加)と、それに引き続く酵素の基質加水分解反応による振動数増加(質量の減少)が経時的に観察されます(図5)。
一般的には、酵素反応は生成物の増加を追跡するため、得られるパラメーターは反応速度定数kcatとミカエリス定数と呼ばれるKm[=(koff +kcat)/kon]のみで、酵素の基質への結合速度定数konや解離速度定数koffは求められないことになります。一方、QCM法では酵素添加直後のΔFの沈み込み(質量増加)は酵素-基質(ES)複合体に対応しており、これまでブラックボックスだったES複合体の生成と減少を経時的に直接追跡できるので、得られる振動数変化(ΔF)のカーブフィッティング解析によって、kcatだけでなくkon、koff、およびKmも求められます。
質量変化を伴う反応であれば、酵素反応だけでなくさまざまな反応追跡にも利用でき、新しい反応動力学解析のツールになると期待できます。
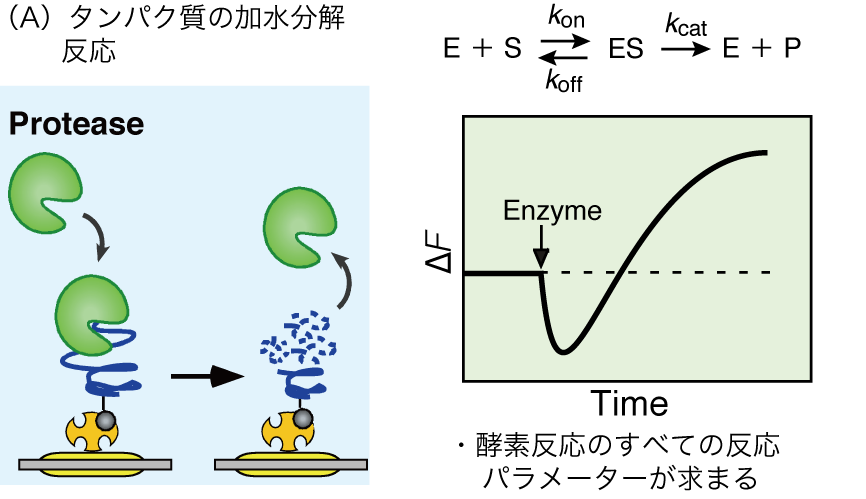
図5 酵素反応の測定例
参考文献
1)バイオセンシングのための水晶発振子マイクロバランス法、講談社、2013年
2)草野 淳、水晶発振回路の設計&実装、Design Wave Magazine、2007年2月号
3)D. A. Buttry and M. D. Ward, Chem. Rev., 92, 1355-1379 (1992)
4)A. Janshoff, H.–J. Galla, and C. Steinem, Angew. Chem. Int. Ed., 39, 4004-4032 (2000)
5)嶋津 克明,現代科学, 6 月号, 14-19 (1998)
6)日本水晶デバイス工業会技術委員会編:「水晶デバイスの解説と応用」,日本水晶デバイス工業会 (2002)
7)日本化学会編:「実験化学講座1(基本操作I)」第4版,丸善,68 (1990)
8)G. Sauerbrey, Z. Phyzik, 155, 206-222 (1959)
8)T. Nomura and A. Minemura, Nippon Kagaku Gaishi, 1621-1628 (1980)
9)P. L. Konash and G. J. Bastiaans, Anal. Chem., 52, 1929-1933 (1980)
10)Y. Okahata, K. Niikura, H. Furusawa, and H. Matsuno, Anal. Sci., 16, 1113-1119 (2000)
11)磯部 俊明、中山 敬一、伊藤 隆司編、「分子間相互作用解析ハンドブック」、 p.137-143, 羊土社 (2007)
12)K. Yazawa, H. Furusawa, and Y. Okahata, J. Biol. Chem., 288, 25969-25981 (2013)
13)H. Furusawa, H. Takano, and Y. Okahata, Anal. Chem., 80, 1005-1011 (2008)
14)S. Takahashi, H. Matsuno, H. Furusawa, and Y. Okahata, J. Biol. Chem., 283, 15023-15030 (2008)
15)小宮山 真編、「酵素利用技術体系」, p.56-62, エヌ・ティ・エス (2010)
16)H. Furusawa, K. Uemura, H. Yoshimine, and Y. Okahata, Analyst, 137, 1334-1337 (2012)
